I came across this question on Quora :
Why was this named as A flat major...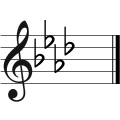
...and this is B flat major?
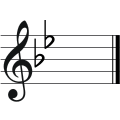
What is the logic behind naming conventions of the musical scales? So we can keep their names in our minds easily?
------------------------------
Its actually one of the more logical aspects of a pretty illogical system. Think of languages, having their own internal logic, like plurals, and conjugation of regular verbs, then there is the mix of civilizations and languages, like in English, which has Germanic, Norse, Latin, French (From the Vikings who learned French and came back to conquer England for a few hundred years) and the exceptions to the logic become a big challenge, because they don't "fit". So music notation is similar, it started out fairly logical, but then was passed around over a 1000 years to dozens of countries and languages.
The "Names" of the notes, in English, French (do re mi) and other languages, are completely arbitrary, but have become so conventional that they stick and become confused with the actual sounds and elements of music they so (poorly) represent. (Go back to English spelling, 26 letter to represent 43 sounds, spelled 151 different ways . . . The spelling is a poor representation of the actual sounds, which is the actual language.)
It becomes a weird salad.
Behind it all is some actual (mathematical!) logic.
First of all, Pythagoras (yes, of the Pythagorean Theorem) discovered about 2500 years ago why notes at an octave sound kind of the same. Their ratios (which he tested with lengths of string or tubular bells) are 2 to 1. In other words, A 440 means that the note vibrates at 440 MHz per second. Up an octave and it is 880 MHz, down an octave and it is 220 MHz. He then tested 2 to 3 ratios (a "perfect fifth" away, or C to G), then corrected down an octave, then tested 3/4, 4/5, 5/6, in a descending order of consonance. These other notes in relation to the base note became a pentatonic (5 note) scale of mostly harmonious notes when played together. Instinctively (not mathematically) most cultures also figured this out. But Western musicians, especially in medieval/renaissance times, found these theories and extrapolated from them.
They went up a fifth from C to find G, then from G to find D, then from D to find A, from A to find E, from E to find B, and then it broke down, because a perfect fifth up was F#. When they started on C and went a perfect fifth DOWN (2/3 ratio) they got to F, not F#, and if they extrapolated downward they ended up with a Bb, not B like in the upward scale. When they adjusted these extrapolations by octave, the ended up with something like a Major Scale, but it was not "perfectly" mathematical, so they tended to round up or down to make scales more singable. They then devised a kind of "circle of fifths" as a way to "modulate" or move to a closely related scale, and of course wanted that to be "perfect" like a circle, but, it wasn't quite, mathematically. (Squaring a circle is never exact, because "pi" is infinite and irrational, while a square is finite and rational but it remained a challenge as did making the musical system "perfect". )
When you take that logic of creating your scale from these mostly harmonic or consonant intervals, and take it to the extreme, you can create an "almost" perfect circular system (Look up "Circle of Fifths")
This allowed people to bring much needed variation into music, by taking the same melody and harmonic section, and repeating it a fifth higher, or lower, then doing that again, and again, then finding a way "home".
But the farther you got away from "home" the more the slight mathematical distortions (like irrational "pi") could not be reconciled, and you would begin to sound "out of tune".
Extrapolating to the farthest key, and you ended up as much as a quarter tone off key. The was the limitation of "Just intonation" or scales built and extrapolated with a "perfect" 2/3 ration or "perfect fifth" (Counting the major scale from C, G is five notes up, so it became a "shorthand" way to refer to the harmonic relationship).
But this ability to "modulate" or migrate to different keys was so powerful, and yet it forced you to retune the instruments if you took it too far, and mid-performance that just broke the experience. What to do?
Like the way we "round off" the days of the year, and then make a "leap year" to correct it, there came a mathematical solution to "round off" the octave, fifth, fourth, etc. to be slightly off, almost imperceptibly off in the tuning, but then avoid the "really off" when you modulated far from the original scale or key.
This tuning system, especially for organs, harpsichords and pianos, became known as the "even tempered" or "Well tempered" tuning system, which consisted of 12 EQUAL half steps (as opposed to a rigid perfect 2/3 ration or "fifth" tuning). This happened and was widely adopted in the Baroque. What it meant, (Back to your original question!) was that a major scale could be built on ANY of those 12 notes, and people could "modulate" or migrate, or move from one related or not so related scale without re-tuning the instrument.
Note: One of the more confusing aspects of musical notation is "enharmonics", i.e, notes like F# and Gb that might have been slightly different with Just intonation, are now identical pitches in even tempered tuning. So it depends did you formulate your scale by going down a series of fifths, and had to flat some notes (go down a half step) to make the scale (flats, b) or up a series of fifths and have to sharp (go up a half step) (sharps, #) Gb and F# are identical major scales but described differently, i.e, did you modulate from Db or from C#? So music, like language, kept a lot of not so logical remnants and then taught the remnants and illogic as "The Way It Is".
Before all this happened one of the most common ways to bring variation to a melody, since you couldn't move to other major scales easily, was to use different "modes". A modal scale simply stays with the Major scale structure, but STARTS on a different note, keeping the same intervals but in a different order. So if you start a Major scale (say C) on the 6th member of the scale (A) that scale is called minor, and is useful because most of the "fifth" relationships still work like a Major scale. Technically, because they were looking at the Greeks, they gave each of these different "modes" a Greek name, of former Greek islands, tribes, etc.
So...
Mode names
Ionian, (Major scale) starts on first note of Major scale, or (I)
C-D-E-F-G-A-B-C
Dorian starts on second note of Major scale, or II
("Scarborough Fair" uses this)
D-E-F-G-A-B-C-D
Phrygian starts on third note of Major scale, or III
("Spain", "Europa" and other Latin American tunes use this)
E-F-G-A-B-C-D-E
Lydian starts on fourth note of Major scale, or IV
("Peaceful Mountain Valleys", from our Piano Wizard Academy uses this)
F-G-A-B-C-D-E-F
Mixolydian starts on fifth note of Major scale, or V
G-A-B-C-D-E-F-G
("Piano Man" and many other pop songs use this section of the scale)
Aeolian (Minor scale) starts on sixth note of Major scale, or VI
A-B-C-D-E-F-G-A
("Dream On", "Eleanor Rigby" "Stairway to Heaven" and many other pop songs, more than half now, use this section of the scale)
Locrian starts on seventh note of Major scale, or VII
B-C-D-E-F-G-A-B
(Very rarely used in pop songs, but often in film scores for its menacing dissonant feel. Note that B to F is NOT a perfect fifth, the only mode that does not have the fifth member "perfect".)
AND, the finale. With the 12 tone, well tempered tuning, that means there are 12 major scales possible, each built on a member of one of the twelve notes (black and white on the piano) of an octave, then the note names of course repeat.
ALSO there are 12 MINOR scales possible built on each of the notes, black or white, on a piano. These are of course all RELATED, or a mode of the Major scales above.
So Bach realized that this meant you could start in any key, and go to related and not so related keys, to any of the modes (7) or any of the other major scales or keys (12) and BACK! (Bach?).
So, to show this off, he wrote 12 major preludes (free form) and 12 major fugues (more strict imitative style pieces, or 24 preludes and fugues, THEN he wrote ANOTHER 24 preludes and fugues in minor keys.
This, the 48 preludes and fugues for the Well (even) Tempered Clavier (early harpsichord) was the genius practice book for Haydn, Mozart, Beethoven, etc., until today, if you want to learn the entire "road-map" of the Western musical tonal system, and how delightful and artful that can be.
And HE named all the major and minor scales by their beginning note name, and that convention, already fairly common, STUCK.
So, the names of the scales, major and minor, are called by the beginning note name of that scale, and the names of modes, (skipping Ionian or Aeolian, which are more likely to be called major and minor respectively) are using the names of ancient Greek places, in tribute to Pythagoras and the Greeks, who first codified and calculated these systems and wrote it down.
THIS was why we created a MUCH SIMPLER way to learn music, using COLORS to represent each note on the chromatic (12 tone) scale, but keeping their fundamental mathematical relationships intact, meaning we can map to anything written in Western music notation (and back!) with 12 colors.
Play piano in minutes with an amazingly simple video game
We built our system to work with any MIDI file, meaning 1000 years of music is available to play, learn and read, through a game, including your favorite pop songs. Bach said, "I just hit the right notes and the right time, and the instrument plays itself."
Simple is genius. Our color coded method makes playing these complex modulating pieces much easier (there is still considerable coordination challenges, but almost zero "deciphering").
That said, music notation, like Chinese characters, which can be rendered phonetically much simpler in roman letters, contains priceless historical, poetic and cultural meaning. It is a crazy system, but there is extra historical, poetic and cultural information embedded in the notation, so we must use the simplicity of the game to transition more easily to the complexity, and make the new generations backwards compatible with the old. So everything we have in a color coded video game transitions the player to reading music notation through 4 intuitive steps, moving them from a concrete simple game to complex reading of even advanced music notation, without pain or trauma, and actually a lot of joy.
Think of it this way. Long time ago, some brilliant philosophers, monks, musicians, composers and other kinds of geniuses hand carved a path up the mountain of music with a machete, and brutal grunt work. We came along and installed a series of ski lifts. Same mountain, lots of fun, but easier to get up to the next level as your skills improve.
Have fun!
Chris Salter


